
Rounded polygon Algorithms, Data Structures and Class Design Delphi
Challenge design: toward universal and efficient cell segmentation algorithms. The primary objective of this challenge was to benchmark universal algorithms capable of accurately segmenting cells.
WPF rounded corners polygon CodeProject
Ideally there'd be one fillet, chamfer, blend component for curves, like with solids, and it'd take point input to select what corners get changed, it'd output a single curve, and it'd have an input that was either fillet/blend radius or chamfer length depending on whether the user selected fillet, blend, or chamfer.
POLYGON CLIPPING PROGRAM IN C SUTHERLAND HODGEMAN ALGORITHM FOR
To do so we first need to turn these 3 points into two vectors. For three points A, B and C we can find the vectors BA and BC by using the following function: // p1 -> first point // p2 -> second point // v -> container that we will fill // we could also not pass v and simply return it function toVec ( p1, p2, v) {.

Using the central corner cutting algorithm, a corner cutting polygon is
I would like to realize beautiful rounded polygons enclosing some nodes. If we use \draw [rounded corners] the resulting polygon does not include our vertices. \coordinate (c\i) at (60*\i:\r) {}; We can shift the center points of the polygon like this, but for each node the direction of shifting changes and had to be calculated.
POLYGON CLIPPING PROGRAM IN C SUTHERLAND HODGEMAN ALGORITHM FOR
Function for rounded polygons? Is there any general function for rounded REGULAR polygons. To be specific, x2 +y2 = 1 x 2 + y 2 = 1 gives a circle ofcourse. Even-numbered higher powers like x10 +y10 = 1 x 10 + y 10 = 1 give a square with rounded corners with the corners becoming sharper as I increase the power.

Polygon simplification by modified DouglasPeucker algorithm. (a) The
Make the corners of a regular rectangular NSImage transparent. You can do that by ANDing the alpha channel of the bitmap or image with an appropriate round-rect mask or mask image. Share
Convex polygon with rounded corners in Swift Few lines of code
Here an algorithm that could work: For each side: Compute the segment's equation. Compute each round corner's circle equation. Compute the intersections between the segment and each circle. The 2 intersection points are the new endpoints for the line segment. This doesn't handle the case where a side is smaller than the rounded corner radius.
POLYGON CLIPPING PROGRAM IN C SUTHERLAND HODGEMAN ALGORITHM FOR
In my previous notebook about how to find the union polygon of overlapping rectangles I've included a polygon corner rounding algorithm as a post-processing step but didn't explain how it worked. In the end, rounding arbitrary polygons essentially comes down to solving the following two things: Drawing a circle using cubic bezier curves, there's a catch Placing a point on a line, at some.

Polygon SweepLine Algorithm
General Polygon Clipper (Free for non-commercial use; has an Objective-C wrapper already) There are others you can find from links off of those pages or using your favorite search engine. Useful search terms include "polygon", "geometry", "union", and "clipping". UPDATE. I understand that you're just drawing one polygon.

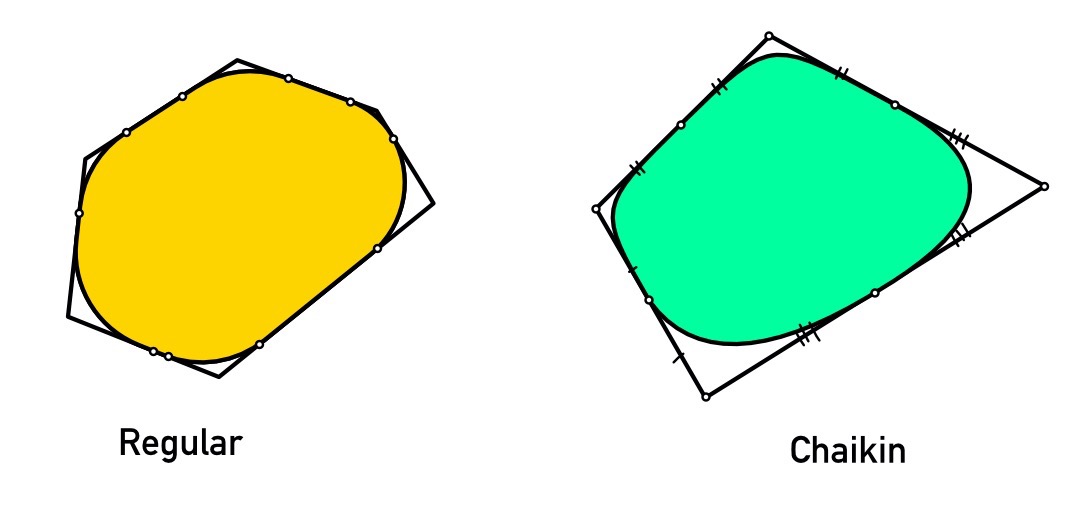
An Algorithm for Polygons with Rounded Corners
This geom is a cousin of ggplot2::geom_polygon() with the added possibility of expanding or contracting the polygon by an absolute amount (e.g. 1 cm). Furthermore, it is possible to round the corners of the polygon, again by an absolute amount. The resulting geom reacts to resizing of the plot, so the expansion/contraction and corner radius will not get distorted. If no expansion/contraction.

Rounded polygon Algorithms, Data Structures and Class Design Delphi
You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window.

objective c Warp array of vertices (polygon) according to the
Quadratic Bezier curves have one control point. The theory says that a quadratic Bezier curve between points P0 and P2 with control point P1 is defined as follows: B (t) = (1 - t)2P0 + 2t (1 - t)P1 + t2P2, where 0 ≤ t ≤ 1 (1) So when t is equal to 0, B (t) will yield P0, when t is equal to 1, B (t) will yield P2, but in every other case.
An Algorithm for Polygons with Rounded Corners
Given shapes like these, which contain just Arcs and lines, I want to round all its corners with certain radius. I know the vertices of the lines & arcs these shapes. I can round the corners of a polygon (when two lines meet to form a corner), but can't figure out how to round a corner formed by an Arc and a Line.

Svgpolygonroundedcorners kenzmaree
1. You know the coordinates of corner points, let it be P 1, P 2 and P: 2. Now you can get vectors from points and angle between vectors: angle = atan(P Y - P 1Y, P X - P 1X) - atan(P Y - P 2Y, P X - P 2X) 3. Get the length of segment between angular point and the points of intersection with the circle.

An Algorithm for Polygons with Rounded Corners
To round the corner of a polygon I could use .round_corners (inner radius, outer radius, number of points) and we use it quite a lot. > round_corners (double rinner,double router,unsigned int n) Is there a way to access only one corner to be rounded? I'm facing the issue to round corner with a different value. Thanks and Best Regards,

Point‐in‐Convex Polygon algorithm with lg complexity Download
If you ever needed to round corners of a polygon — not a rectangle, in which case at least you have a CSS rule "border-radius," but an n-polygon like star or a triangle — you probably googled for such an algorithm, an npm package, or a git repo. In my case, I found a few (lib svg-round-corners, stackoverflow discussion, algo1, algo2 ), but.